# A. Rings and Rods (opens new window)
Count the number of rings on each rod.
DETAILS
def countPoints(self, A: str) -> int:
res = [set() for i in range(10)]
n = len(A) // 2
for i in range(n):
idx = int(A[i * 2 + 1])
ch = A[i * 2]
res[idx].add(ch)
ans = 0
for i in range(10):
if len(res[i]) == 3:
ans += 1
return ans
# B. Sum of Subarray Ranges (opens new window)
DETAILS
def subArrayRanges(self, A: List[int]) -> int:
ans, n = 0, len(A)
for i in range(n - 1):
mi, ma = A[i], A[i]
for j in range(i + 1, n):
mi = min(mi, A[j])
ma = max(ma, A[j])
ans += ma - mi
return ans
# B. Watering Plants II (opens new window)
Two pointers.
DETAILS
def minimumRefill(self, P: List[int], A: int, B: int) -> int:
n = len(P)
ans = 0
cura, curb = A, B
i, j = 0, n - 1
while i < j:
if cura >= P[i]:
cura -= P[i]
else:
cura = A - P[i]
ans += 1
if curb >= P[j]:
curb -= P[j]
else:
curb = B - P[j]
ans += 1
i += 1
j -= 1
if i > j:
return ans
else:
if max(curb, cura) < P[i]:
ans += 1
return ans
# C. Maximum Fruits Harvested After at Most K Steps (opens new window)
Please refer to This LC Discussion (opens new window) for my solutions in English.
我们需要找出走了k距离后能采到的最多水果,为了尽量采集更多的水果,我们要选择少走重复的路,所以最佳的路线只能可能是以下两种:
- 向左走一段路,然后折返向右走一段路
- 向右走一段路,然后折返向左走一段路
(一直向左(右)走属于上述的特例,相当于折返后走了距离为0的路)
# 解法一, Prefix + Binary Search
从startPos出发,向右走到每个有水果的地点,算一下如果此时折返向左走,我们可以越过startPos到左边的距离,以及这个距离内能采多少水果。
这需要建立从startPos开始向左的prefix sum数组。
同理,计算先向左之后向右的各种情况。
DETAILS
def maxTotalFruits(self, A: List[List[int]], pos: int, k: int) -> int:
amt = {}
for a, b in A:
amt[a] = b
# Every position with fruit except the start position.
position = [a for a, b in A if a != pos]
lft, rgt, n = [], [], len(position)
idx = bisect.bisect_right(position, pos)
# Right pre-sum
cur_f = 0
for i in range(idx, n):
cur_pos = position[i]
cur_f += amt[cur_pos]
rgt.append([cur_pos - pos, cur_f])
# Left pre-sum
cur_f = 0
for i in range(idx - 1, -1, -1):
cur_pos = position[i]
cur_f += amt[cur_pos]
lft.append([pos - cur_pos, cur_f])
# Go right then turn left
ans = 0
for r_dist, r_f in rgt:
if r_dist <= k:
cur_f = r_f
l_dist = k - 2 * r_dist
if l_dist > 0: # Check fruit collected from the left side.
idx = bisect.bisect_right(lft, [l_dist, float('inf')])
if idx > 0:
cur_f += lft[idx - 1][1]
ans = max(ans, cur_f)
# Go left then turn right
for l_dist, l_f in lft:
if l_dist <= k:
cur_f = l_f
r_dist = k - 2 * l_dist
if r_dist > 0: # Check fruit collected from the right side.
idx = bisect.bisect_right(rgt, [r_dist, float('inf')])
if idx > 0:
cur_f += rgt[idx - 1][1]
ans = max(ans, cur_f)
return ans + amt.get(pos, 0) # Add fruit collected at the start position.
# 解法二, Prefix
直接建立整段路上水果总数的prefix sum,用解法一的方式求出我们到达的最左点left和最右点right,算出[left, right]之间所有的水果数量即可。
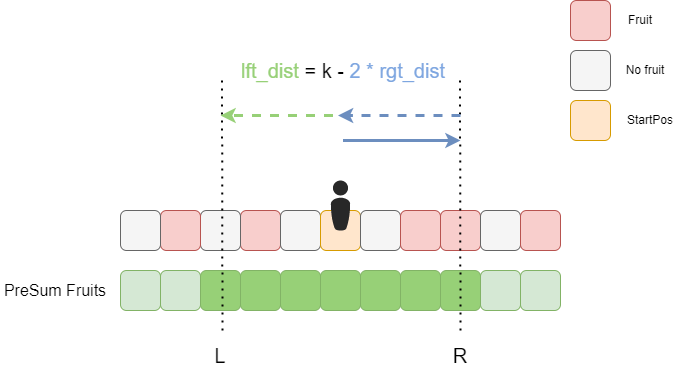
DETAILS
def maxTotalFruits(self, A: List[List[int]], pos: int, k: int) -> int:
r_b = max(pos, A[-1][0]) # right boundary.
amt = [0] * (1 + r_b)
for a, b in A:
amt[a] = b
presum = [0] + list(itertools.accumulate(amt)) # prefix sum
ans = 0
for r_dist in range(min(k, r_b - pos) + 1): # The right distance to start position.
l_dist = max(0, k - 2 * r_dist) # If we turn around, how far we can go left beyond start position.
l_pos, r_pos = max(0, pos - l_dist), pos + r_dist # The leftmost and rightmost position we can reach.
ans = max(ans, presum[r_pos + 1] - presum[l_pos]) # Get overall fruits within this range from presum.
for l_dist in range(min(k, pos) + 1):
r_dist = max(0, k - 2 * l_dist)
l_pos, r_pos = pos - l_dist, min(r_b, pos + r_dist)
ans = max(ans, presum[r_pos + 1] - presum[l_pos])
return ans