A. Largest Number After Digit Swaps by Parity (opens new window)

DETAILS

public int largestInteger(int num) {
        char[] ans = String.valueOf(num).toCharArray();
        int n = ans.length;
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                if (ans[j] > ans[i] && (ans[j] - ans[i]) % 2 == 0) {
                    char tmp = ans[i];
                    ans[i] = ans[j];
                    ans[j] = tmp;
                }
            }
        }
        return Integer.parseInt(new String(ans));
    }

def largestInteger(self, num: int) -> int:
        ans = ""
        even, odd = [], []
        idx_even = []
        for i, ch in enumerate(str(num)):
            if int(ch) % 2:
                odd.append(ch)
            else:
                even.append(ch)
                idx_even.append(i)
        odd.sort(reverse = True)
        even.sort(reverse = True)
        
        i, j = 0, 0
        for k in range(len(str(num))):
            if k in idx_even:
                ans += even[j]
                j += 1
            else:
                ans += odd[i]
                i += 1
        return int(ans)

B. Minimize Result by Adding Parentheses to Expression (opens new window)

Find all workable positions and get the answer of that expression.

DETAILS

def minimizeResult(self, E: str) -> str:
        n = len(E)
        pos = E.find("+")
        ans = math.inf
        exp = [-1, -1]
        for lft in range(pos):
            for rgt in range(pos + 2, n + 1):
                if lft == 0:
                    a = 1
                else:
                    a = int(E[:lft])
                if rgt == n:
                    b = 1
                else:
                    b = int(E[rgt:])
                
                cur = a * b * eval(E[lft:rgt])
                if cur < ans:
                    ans = cur
                    exp = [lft, rgt]
        return E[:exp[0]] + "(" + E[exp[0]:exp[1]] + ")" + E[exp[1]:]

C. Maximum Product After K Increments (opens new window)

Priority Queue, only increment the smallest integer by 1 each time.

DETAILS

def maximumProduct(self, A: List[int], k: int) -> int:
        heapq.heapify(A)
        for _ in range(k):
            cur = heapq.heappop(A)
            heapq.heappush(A, cur + 1)  
        ans = 1
        if A[0] == 0: 
            return 0
        for a in A:
            ans *= a
            ans %= (10 ** 9 + 7)
        return ans

D. Maximum Total Beauty of the Gardens (opens new window)

Please refer to This LC Discussion (opens new window) for my solutions in English.

额外的花数量有限，如果我们把更多的花用来填满花园：

• 我们会获得更多的【满花园】，full分数增加
• 说明【最小花园】的花数量会降低，part分数降低

如图所示，如果我们把一部分花去多填满一个花园，【最小花园】的花数会降低。

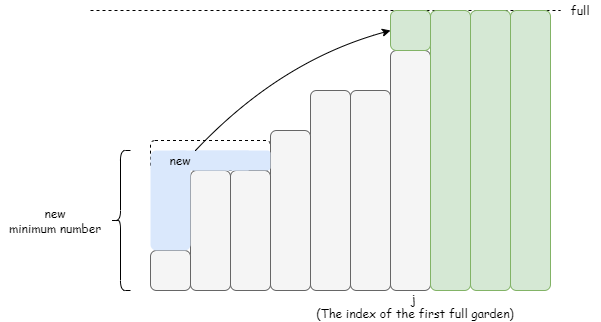
所以分数的最大值分布并没有一个明显的规律，我们需要检查所有的种花方案，找出其中分数的最大值。

显然，为了用尽量少的花去填满花园，我们可以从已经种花最多的花园开始填。

如上图所示，我们填满了4个花园，剩下一些花，那么如何快速地算出【最小花园】的花数？

我们可以建立一个数列cost, 其中cost[i]是把【最小花园】的花数提升到A[i]的花数。

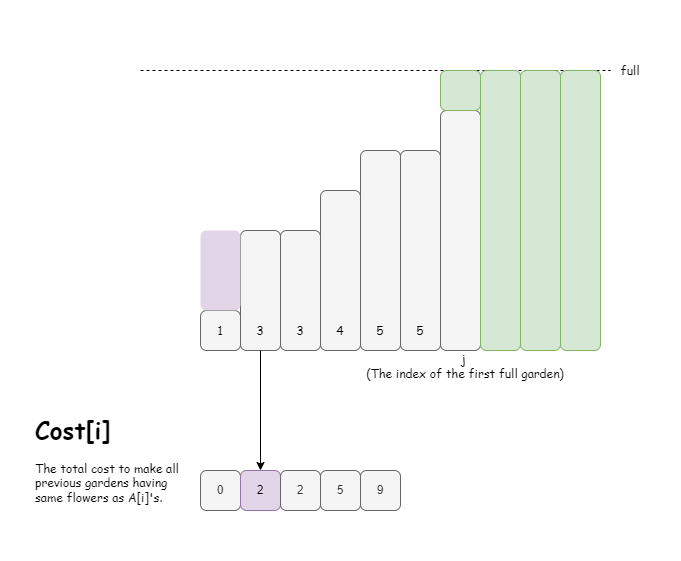
这个数列是非递减的，因此我们可以把做二分查找，查询剩下的花足够把【最小花园】提升多少。

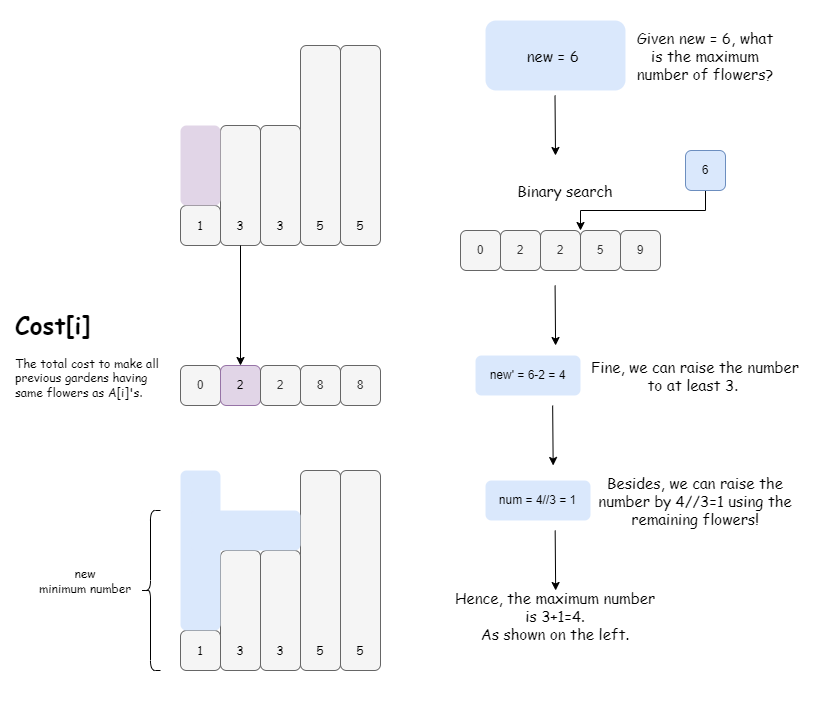
DETAILS

def maximumBeauty(self, A: List[int], new: int, t: int, full: int, part: int) -> int:
        A = [min(t, a) for a in A]
        A.sort()
		
		# Two edge cases
        if min(A) == t: return full * len(A)
        if new >= t * len(A) - sum(A):
            return max(full*len(A), full*(len(A)-1) + part*(t-1))
        
		# Build the array `cost`.
        cost = [0]
        for i in range(1, len(A)):
            pre = cost[-1]
            cost.append(pre + i * (A[i] - A[i - 1]))

		# Since there might be some gardens having `target` flowers already, we will skip them.
        j = len(A) - 1
        while A[j] == t:
            j -= 1
        
		# Start the iteration
        ans = 0
        while new >= 0:
		
			# idx stands for the first `j` gardens, notice a edge case might happen.
            idx = min(j, bisect_right(cost, new) - 1)
			
			# bar is the current minimum flower in the incomplete garden
            bar = A[idx] + (new - cost[idx]) // (idx + 1)
			
            ans = max(ans, bar * part + full *(len(A) - j - 1))
            
			# Now we would like to complete garden j, thus deduct the cost for garden j 
			# from new and move on to the previous(next) incomplete garden!
			new -= (t - A[j])
            j -= 1
            
        return ans

DETAILS