A. Calculate Digit Sum of a String (opens new window)

Repeat Divide, Replace, Merge until the length of s is no larger than k.

DETAILS

def digitSum(self, s: str, k: int) -> str:
        while len(s) > k:
            cur = [s[i: i + k] for i in range(0, len(s), k)]
            s = ""
            for st in cur:
                tmp = 0
                for ch in st:
                    tmp += int(ch)
                s += str(tmp)
        return s

B. Minimum Rounds to Complete All Tasks (opens new window)

Groupby.

DETAILS

def minimumRounds(self, A: List[int]) -> int:
        tmp = [len(list(g)) for k, g in itertools.groupby(sorted(A))]
        ans = 0
        for n in tmp:
            if n < 2:
                return -1
            elif n == 4:
                ans += 2
            elif n % 3 == 0:
                ans += n // 3
            else:
                ans += n // 3 + 1
        return ans

C. Maximum Trailing Zeros in a Cornered Path (opens new window)

Please refer to This LC Discussion (opens new window) for my solutions in English.

Prefix，对于每个位置(i, j)， 有四种可能的路线，我们需要找到从当前位置出发，到上、下、左、右边界的四条路径上所有数的乘积内有多少2, 5。这两个因子的数量决定了乘积后缀0的数量。

DETAILS

def maxTrailingZeros(self, A: List[List[int]]) -> int:
        m, n = len(A), len(A[0])
        left = [[[0, 0] for _ in range(n)] for _ in range(m)]
        top = [[[0, 0] for _ in range(n)] for _ in range(m)]
     
        def helper(num):
            a, b = 0, 0
            while num % 2 == 0:
                num //= 2
                a += 1
            while num % 5 == 0:
                num //= 5
                b += 1
            return [a, b]
        
        for i in range(m):
            for j in range(n):
                if j == 0:
                    left[i][j] = helper(A[i][j])
                else:
                    a, b = helper(A[i][j])
                    left[i][j][0] = left[i][j - 1][0] + a
                    left[i][j][1] = left[i][j - 1][1] + b
        for j in range(n):
            for i in range(m):
                if i == 0:
                    top[i][j] = helper(A[i][j])
                else:
                    a, b, = helper(A[i][j])
                    top[i][j][0] = top[i - 1][j][0] + a               
                    top[i][j][1] = top[i - 1][j][1] + b

        ans = 0
        for i in range(m):
            for j in range(n):
                a, b = top[m - 1][j]
                d, e= left[i][n - 1]
                x, y = helper(A[i][j])
                a1, b1 = top[i][j]
                a2, b2= left[i][j]
                tmp = [a1 + a2 - x, b1 + b2 - y]
                ans = max(ans, min(tmp))
                tmp = [d - a2 + a1, e - b2 + b1]
                ans = max(ans, min(tmp))             
                tmp = [a - a1 + a2, b - b1 + b2]
                ans = max(ans, min(tmp))
                tmp = [a + d - a1 - a2 + x, b + e - b1 - b2 + y]
                ans = max(ans, min(tmp))
        return ans

D. Longest Path With Different Adjacent Characters (opens new window)

Please refer to This LC Discussion (opens new window) for my solutions in English.

BFS. Each chain consists of one parent node and at most two longest chains from its child nodes.

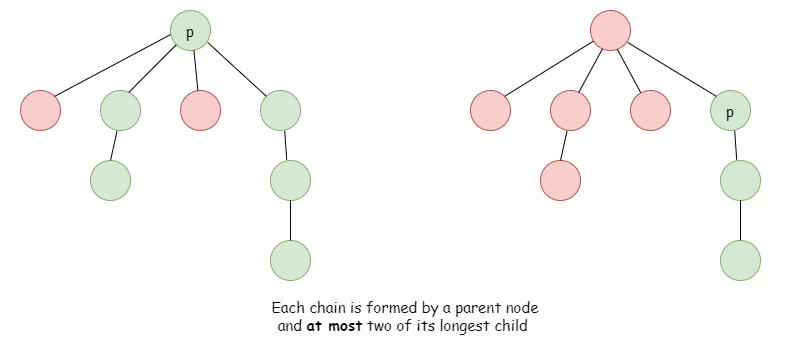
Thus for node a, we save the longest 2 chains from a's child nodes.

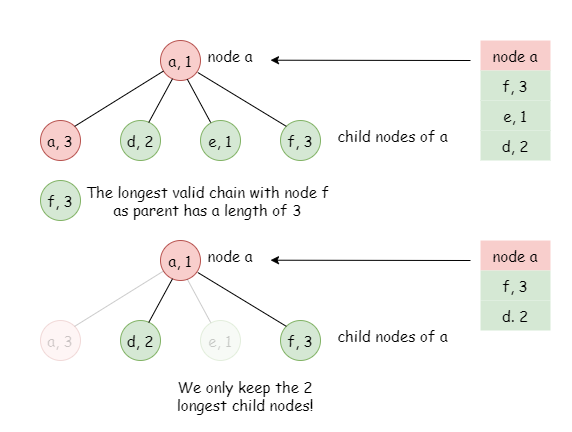
For example

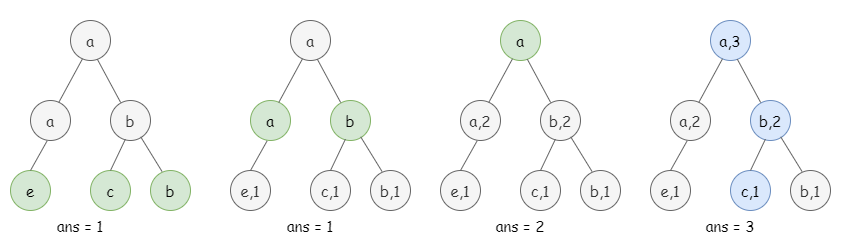
DETAILS

def longestPath(self, A: List[int], s: str) -> int:
        n = len(A)
        child_num = [0] * n
        
        # count the number of children for each node
        for a in A[1:]:
            child_num[a] += 1
        
        # The longest valid chain with node i as parent.
        longest = [[0] for _ in range(n)]
        
        # Add all leaf nodes to deque
		# [current node, the maximum length end by this node]
        dq = collections.deque()
        for i in range(n):
            if child_num[i] == 0:
                dq.append([i, 1])
        
        ans = 1
        while dq:
            cur_i, cur_l = dq.popleft()
            cur_p = A[cur_i]
            
            # Minus the number of unvisited child node by 1
            child_num[cur_p] -= 1
            
            # If the child has different char with parent
            if s[cur_p] != s[cur_i]:
                bisect.insort_right(longest[cur_p], cur_l)
                if len(longest[cur_p]) > 2:
                    longest[cur_p].pop(0)
                    
            # If the parent has 0 univisited child, meaning it also
            # become a child node, add it to deque.
            if child_num[cur_p] == 0:
                ans = max(ans, 1 + sum(longest[cur_p][-2:]))
                dq.append([cur_p, 1 + longest[cur_p][-1]])
                
        return ans