A. Largest 3-Same-Digit Number in String (opens new window)

DETAILS

def largestGoodInteger(self, S: str) -> str:
        ans = ""
        n = len(S)
        for i in range(n - 2):
            if S[i] == S[i + 1] == S[i + 2]:
                ans = max(ans, S[i:i +3])
        return ans

B. Count Nodes Equal to Average of Subtree (opens new window)

DFS, get the number of nodes and the sum of nodes value of its subtree.

DETAILS

def averageOfSubtree(self, root: Optional[TreeNode]) -> int:
        self.ans = 0
        def dfs(root):
            if not root: 
                return 0, 0
            lnode, lsum = dfs(root.left)
            rnode, rsum = dfs(root.right)
            curnode = 1 + lnode + rnode
            cursum = root.val + lsum + rsum
            if math.floor(cursum / curnode) == root.val:
                self.ans += 1
            return curnode, cursum
        dfs(root)
        return self.ans

C. Count Number of Texts (opens new window)

1-d DP.

DETAILS

def countTexts(self, S: str) -> int:
        tmp = [(a, len(list(g))) for a, g in itertools.groupby(S)]
        mod, n = 10 ** 9 + 7, max(10, len(S))
        dp3, dp4 = [0] * n, [0] * n
        dp3[0], dp3[1], dp3[2] = 1, 2, 4
        dp4[0], dp4[1], dp4[2], dp4[3] = 1, 2, 4, 8

        for i in range(3, n):
            dp3[i] = dp3[i-1] + dp3[i-2] + dp3[i-3]
            dp3[i] %= mod
        for i in range(4,n):
            dp4[i] = dp4[i-1]+dp4[i-2]+dp4[i-3]+dp4[i-4]
            dp4[i] %= mod

        ans = 1
        for a, le in tmp:
            if a in ["7","9"]:
                ans *= dp4[le - 1]
            else:
                ans *= dp3[le - 1]
            ans %= mod
        return ans

D. Check if There Is a Valid Parentheses String Path (opens new window)

DP. Every valid path must:

• Have prefix sum = 0 at bottom right cell.
• The prefix never goes below 0.

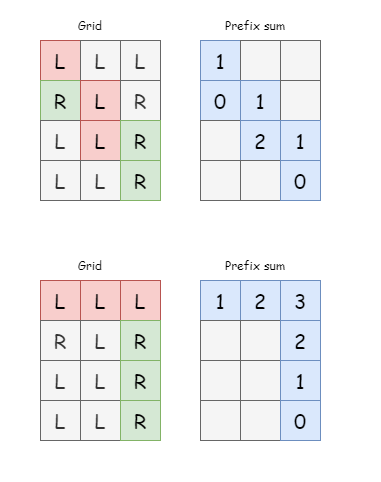
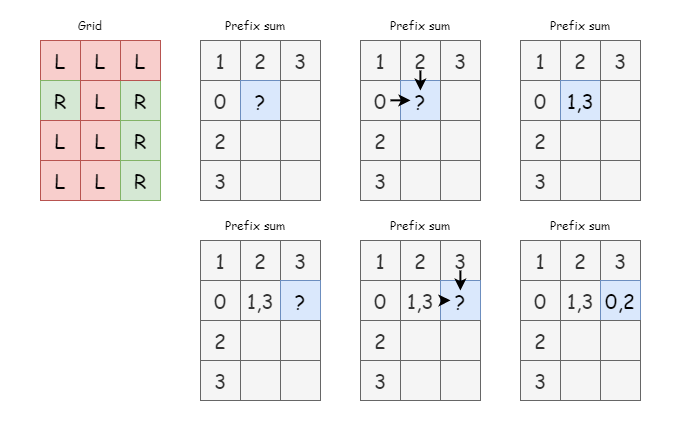
Take a look at how we build the bottom up DP matrix.

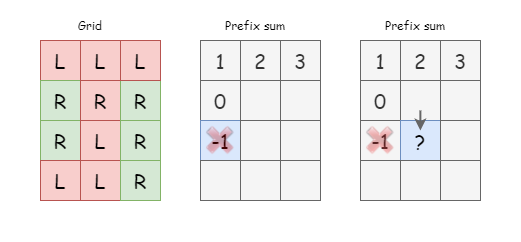
If the prefix sum of a cell goes below 0, we will not use this cell in further iteration.

DETAILS

def hasValidPath(self, grids: List[List[str]]) -> bool:
        rows, cols = len(grids), len(grids[0])
        if grids[0][0]==")" or (rows + cols) % 2 == 0:
            return False
        DP = [[1] * cols for _ in range(rows)]
        for i in range(rows):
            for j in range(cols):
                DP[i][j] = set()
        DP[0][0].add(1)
        num = 1
        for i in range(1, rows):
            if grids[i][0] == "(": num += 1
            else: num -= 1
            if num < 0: break
            else: DP[i][0].add(num)
        num = 1
        for i in range(1, cols):
            if grids[0][i] == "(": num += 1
            else: num -= 1
            if num < 0: break
            else: DP[0][i].add(num)
        for i in range(1, rows):
            for j in range(1, cols):
                if (not DP[i - 1][j]) and (not DP[i][j - 1]):
                    continue
                curset = DP[i - 1][j] | DP[i][j - 1]
                if grids[i][j] == "(":
                    for a in curset: DP[i][j].add(a + 1)
                else:
                    for a in curset:
                        if a > 0: 
                            DP[i][j].add(a - 1)
        return 0 in DP[rows - 1][cols - 1]