A. Decode the Message (opens new window)

Collect key-val pairs of each unique characters. Then translate the message using all the pairs.

DETAILS

def decodeMessage(self, key: str, message: str) -> str:
        d, n, ans = {}, 0, ""
        for ch in key:
            if ch != " " and ch not in d:
                d[ch] = chr(n + ord('a'))
                n += 1
        for ch in message:
            ans += d[ch] if ch != ' ' else ' '
        return ans

B. Spiral Matrix IV (opens new window)

Let the pointer (0, 0) stands for our current position in the matrix and the original directions is to the right. If the pointer is out of boundary, or represent a cell that has already been updated, then we change the direction of the pointer.

DETAILS

def spiralMatrix(self, m: int, n: int, head: Optional[ListNode]) -> List[List[int]]:
        A = [[-1] * n for _ in range(m)]
        dirs = [[0, 1], [1, 0], [0, -1], [-1, 0]]
        i, j, idx = 0, 0, 0
        while head:
            A[i][j], head = head.val, head.next
            if not head: return A
            if i + dirs[idx][0] < 0 or i + dirs[idx][0] >= m or j + dirs[idx][1] < 0 or j + dirs[idx][1] >= n or A[i + dirs[idx][0]][j + dirs[idx][1]] != -1:
                idx += 1
                idx %= 4
            i += dirs[idx][0]
            j += dirs[idx][1]

C. Number of People Aware of a Secret (opens new window)

Please refer to This LC Discussion (opens new window) for my solutions in English.

We only focus on the number of people who first know the secret on each day.

Solution 1. O(N^2)

Just update the number of people in the future days that got the message from people on day i.

DETAILS

def peopleAwareOfSecret(self, n: int, dd: int, ff: int) -> int:
        dp, mod, ans = [0] * 1001, 1000000007, 0
        dp[1] = 1
        for d in range(1, n + 1):
            if dp[d] > 0:
                for nxt in range(d + dd, min(d + ff, 1001)):
                    dp[nxt] += dp[d]
        for d in range(1, n + 1):
            if d + ff > n:
                ans += dp[d]
        return ans % mod

Solution 2. O(N)

Use prefix sum.

DETAILS

def peopleAwareOfSecret(self, n: int, dd: int, ff: int) -> int:
        dp, mod = [0] * 1002, 1000000007
        dp[1], dp[2] = 1, -1
        cur, ans = 0, 0
        
        for d in range(1, n + 1):
            cur += dp[d]
            if d + ff > n:
                ans += cur
            if cur > 0:
                dp[min(d + dd, 1001)] += cur
                dp[min(d + ff, 1001)] -= cur

        return ans % mod

D. Number of Increasing Paths in a Grid (opens new window)

Please refer to This LC Discussion (opens new window) for my solutions in English.

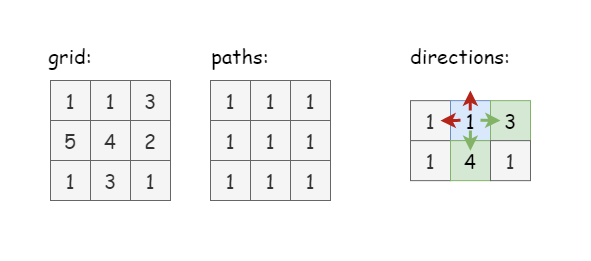
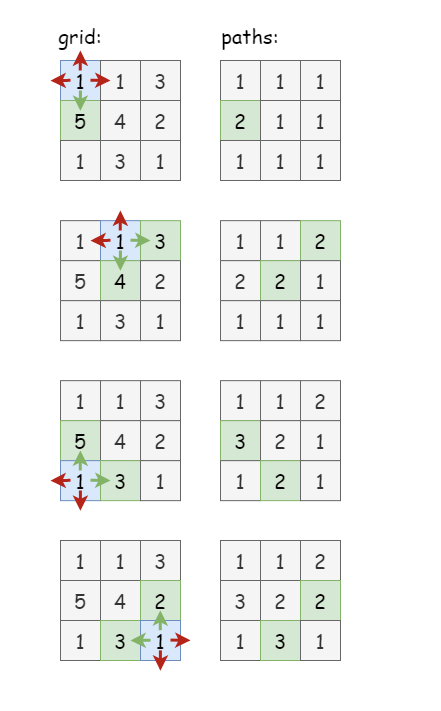
DETAILS

def countPaths(self, G: List[List[int]]) -> int:
        m, n, mod = len(G), len(G[0]), 1000000007
        A, heap = [[1] * n for _ in range(m)], []
        dirs = [[1, 0], [0, 1], [-1, 0], [0, -1]]
        
        for i in range(m):
            for j in range(n):
                heap.append([G[i][j], i, j])
        heapq.heapify(heap)
        
        while heap:
            _, i, j = heapq.heappop(heap)
            for d in dirs:
                ii, jj = i + d[0], j + d[1]
                if 0 <= ii < m and 0 <= jj < n and G[ii][jj] > G[i][j]:
                    A[ii][jj] = (A[ii][jj] + A[i][j]) % mod

        return sum(sum(a) for a in A) % mod