A. Find the K-Beauty of a Number (opens new window)

DETAILS

int divisorSubstrings(int N, int k) {
        string S = to_string(N);
        int ans = 0, n = S.size();
        for (int i = 0; i < n - k + 1; ++i)
            if (stoi(S.substr(i, k)) && N % stoi(S.substr(i, k)) == 0)
                ans++;
        return ans;
    }

B. Number of Ways to Split Array (opens new window)

Prefix sum.

DETAILS

int waysToSplitArray(vector<int>& A) {
        vector<long> pre{0};
        int ans = 0, n = A.size();
        long cur = 0;
        for (auto a : A) {
            cur += a;
            pre.push_back(cur);
        }
        long ssum = pre.back();
        for (int i = 1; i < n; ++i)
            if (pre[i] * 2 >= ssum)
                ans++;
        return ans;        
    }

C. Maximum White Tiles Covered by a Carpet (opens new window)

Please refer to This LC Discussion (opens new window) for my solutions in English.

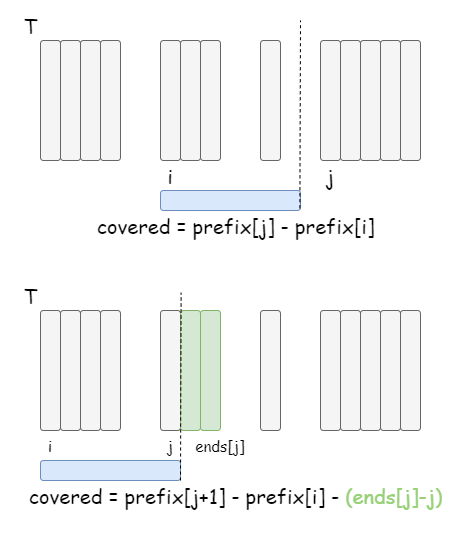
贪心法，把地毯跟每块tile最左端i对齐，利用二分法（或者双指针）寻找地毯右侧j的位置，利用prefix sum得到地毯(i, j)之间覆盖tile的数量。如下图所示，有四片tile，我们共计要尝试对齐四次。

对齐左边后，找地毯最右端的位置，这个位置指的是**最右端落在第几片tile上？或者落在哪两片tile之间的缝隙？**两种情况对应不同的计算被覆盖的tile的数量

DETAILS

def maximumWhiteTiles(self, T: List[List[int]], clen: int) -> int:
        T.sort()
        pref = [0] + list(itertools.accumulate(r - l + 1 for l, r in T))
        ends = [r for _, r in T]
        
        n = len(ends)
        j, ans = 0, 0
        
        for i in range(n):
            l, _ = T[i]                        # Carpet starts from the begining of each range
            r = min(ends[-1], l + clen - 1)    # The rightmost index having tile is ends[-1]

            while j < n and ends[j] < r:       # While the WHOLE current range is covered by carpet
                j += 1
            
            # Two cases: 
            if T[j][0] > r:    # If the right end of the carpet doesn't reach the j-th range.
                ans = max(ans, pref[j] - pref[i])
            else:              # If the right end of the carpet covers part of the j-th range.
                ans = max(ans, pref[j + 1] - pref[i] - ends[j] + r)
            
        return ans

D. Substring With Largest Variance (opens new window)

DETAILS

class Solution {
public:
    int largestVariance(string S) {
        int n = S.size(), ans = 0;
        vector<vector<int>> dp(26, vector<int>(n + 1, 0));
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < 26; ++j) {
                if (j == S[i] - 'a')
                    dp[j][i + 1] = dp[j][i] + 1;
                else
                    dp[j][i + 1] = dp[j][i];
            }
        }
        
        for (int i = 0; i < 26; ++i) {
            for (int j = 0; j < 26; ++j) {
                if (i == j || dp[i][n] == 0 || dp[j][n] == 0)
                    continue;
                int af = 0, bf = 0;
                for (int k = 0; k < n; ++k) {
                    if (S[k] - 'a' == i) {
                        af++;
                    } else if (S[k] - 'a' == j) {
                        bf++;
                    }
                    
                    if (af > 0)
                        ans = max(ans, bf - af);
                    if (bf < af && dp[i][n] > dp[i][k + 1]) {
                        af = 0;
                        bf = 0;
                    }  
                }
            }
        }
        return ans;
    }
};