A. Count Days Spent Together (opens new window)

Please refer to This LC Discussion (opens new window) for my solution in English.

本质是找两个区间的交集，但是计算天数时可能会有点麻烦。

两个区间的交集，取决于较晚的开始时间，和较早的结束时间。

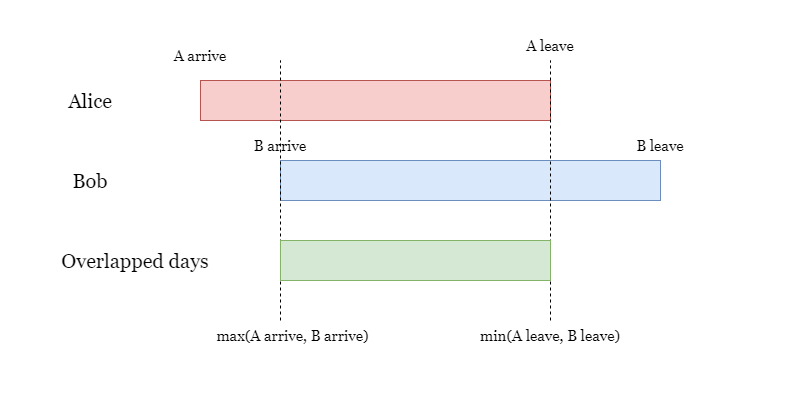
我们不直接计算区间内的天数，而是分别计算两个日期距离年初(1月1日)的天数差，两个天数差相减，也可以得到区间内天数。

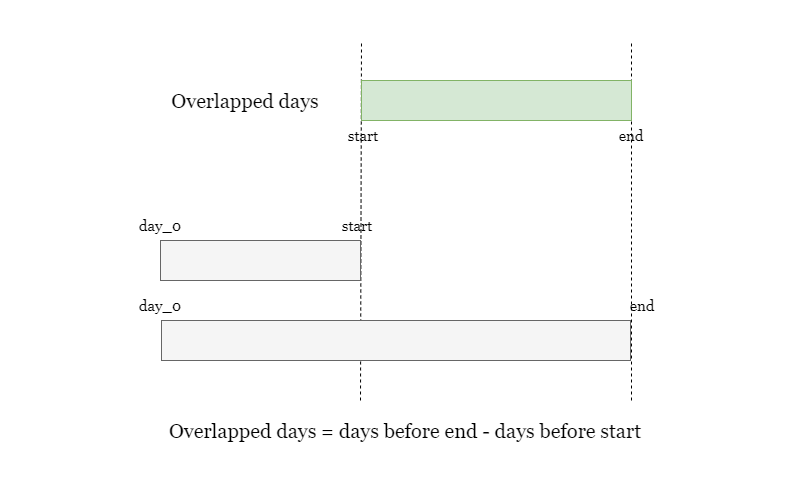
怎么计算距离年初的天数差？整月的天数，加上不足一个月的天数。

例子：

DETAILS

def countDaysTogether(self, aa: str, la: str, ab: str, lb: str) -> int:
        D = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]
        
        def helper(days):
            return int(days[-2:]) + sum(D[:int(days[:2]) - 1])
        
        return max(0, helper(min(la, lb)) - helper(max(aa, ab)) + 1)

B. Maximum Matching of Players With Trainers (opens new window)

Greedy, sort players and trainers by ability.

Start with the player with the smallest ability, try to find a trainer for him. Move to the next player after finding a trainer for the previous player.

DETAILS

def matchPlayersAndTrainers(self, P: List[int], T: List[int]) -> int:
        P.sort()
        T.sort()
        ans, i, j = 0, 0, 0
        while i < len(P) and j < len(T):
            if P[i] <= T[j]:
                i += 1
                ans += 1
            j += 1
        return ans

C. Smallest Subarrays With Maximum Bitwise OR (opens new window)

Sliding window.

DETAILS

def smallestSubarrays(self, A: List[int]) -> List[int]:
        def helper(arr):
            curr = 0
            for i, a in enumerate(arr):
                if a: curr += (1 << i)
            return curr
        
        ans, n, start, number, tmp = [0] * len(A), len(A), 0, 0, [0] * len(A)
        for a in A: start |= a

        for i in range(n - 1, -1, -1):
            number |= A[i]
            tmp[i] = number
        
        c = [[0] * 30 for _ in range(n)]
        for i in range(n):
            k = 0
            while A[i]:
                if A[i] & 1: c[i][k] += 1
                A[i] >>= 1
                k += 1

        curr, j = [0] * 30, 0
        for i in range(n):
            while helper(curr) != tmp[i]:
                for k in range(30): curr[k] += c[j][k]
                j += 1
            ans[i] = max(1, j - i)
            for k in range(30): curr[k] -= c[i][k]
            
        return ans

D. Minimum Money Required Before Transactions (opens new window)

Please refer to This LC Discussion (opens new window) for my solution in English.

Greedy.

把transactions根据cost和cashback的大小关系分成两部分，盈利的和亏损的。

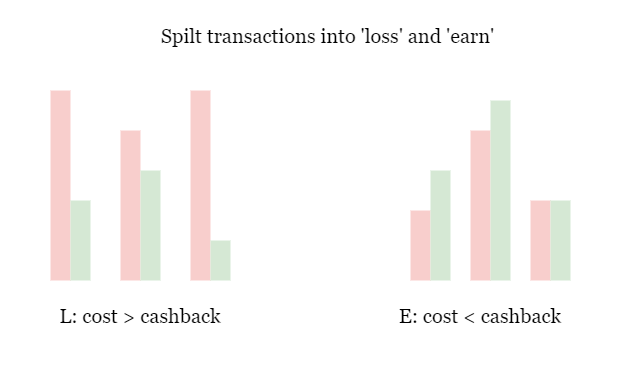
由于盈利的操作不会让budget减少，我们要把它们放到最后来处理：先亏损，后盈利。这样一来对于初始budget的要求才最高。

对于每一个亏损操作，我们既要保证当前的budget足够支付这个操作的cost，也要保证操作后的cashback可以应对下一个操作。

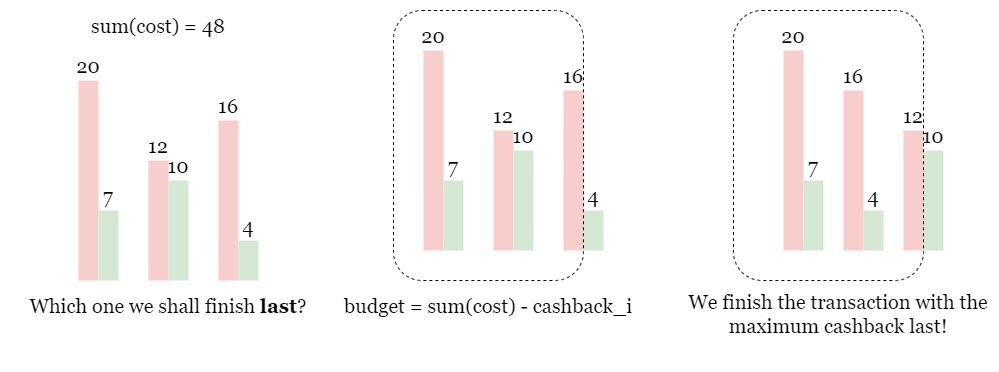
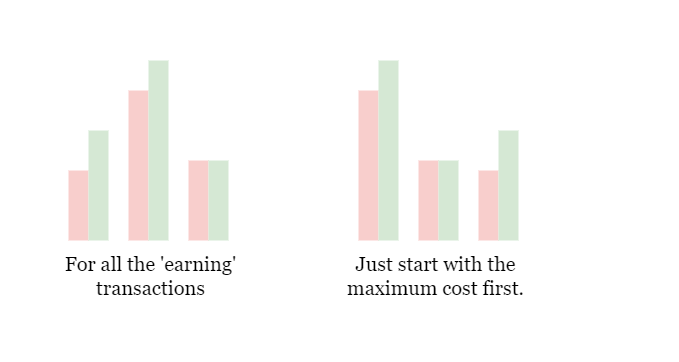
接下来处理盈利操作，因为盈利操作下budget是不会减少的，那么第一个操作前budget是最低的，如果这个时候可以满足cost最高的操作，那么接下来的操作就都可以满足了。

DETAILS

def minimumMoney(self, A: List[List[int]]) -> int:
        # Splist transcations into two groups and sort according to the order.
        L, E = [a for a in A if a[0] > a[1]], [a for a in A if a[0] <= a[1]]
        L.sort(key = lambda x:  x[1])
        
        # budget: minimum budget we have met.
        # curr: current budget we have.
        budget, curr = 0, 0
        
        for a, b in L:
            curr -= a
            budget = min(budget, curr)
            curr += b
        
        if E:
            curr -= max(e[0] for e in E)
            budget = min(budget, curr)

        return -budget